Genetic control of number of flowers and pod set in common bean
Received: May 14, 2017
Accepted: August 14, 2017
Published: September 21, 2017
Genet.Mol.Res. 16(3): gmr16039723
DOI: 10.4238/gmr16039723
Abstract
This article aimed to study the genetic control of some flowers and pod set of common bean and to verify if its estimate varies with environmental conditions and gene pool. A complete diallel was used among six lines, but no reciprocal ones. The treatments were evaluated in three harvests/generations - F2, F3, and F4 - in 2015/2016, in a randomized complete block design with four replications. The plot consisted of 3 lines with 4 m. In the center line, a receptacle to collect the aborted flowers/pods was placed. The traits considered were the number of flowers/plant (N), the percentage of pod set (V), and the production of grain/plant (W). A joint diallel analysis was performed, and the correlations between N, V, and W were estimated. N was 31.9 on average, and V was 40.4%. The average of Mesoamerican parents, for N and V, was higher than for Andean. Specific combining ability explained most of the variation for N, evidencing predominance of dominance effect. For V, specific combining ability was slightly lower than general combining ability, indicating additive loci and also dominance effects.These two traits were very influenced by environment and should be considered a strategy for greater grain yield stability of common bean.
Introduction
The search for a strategy that can increase cultivated plant grain yield is a challenge to be overcome by breeders. In the case of common bean and other legumes, grain yield depends on several biotic and abiotic factors, and consequently, the yield potential of plants is almost never obtained due to the stresses.
Common bean yield potential (W) is dependent on the number of pods (X), the number of seeds per pod (Y), and the average weight of grains (Z). The product X . Y . Z = W. The contribution of each of these primary components of production is variable; however, in numerous situations, the number of pods/plant has been shown to be the most important (Zilio et al., 2011; Guilherme et al., 2014).
The number of pods, in turn, is dependent on the numbers of flowers (N) produced by the plant and the percentage of pod set (V), i.e., the proportion of flowers that gives rise to pods. Usually, the number of flowers per plant is much higher than that of pods, and this means that the percentage of pod set is almost always small. As a consequence, the plant is not able to express its full potential, as already mentioned, because the biotic and abiotic stresses affect the percentage of a pod set.
Unfortunately, there are not many reports estimating the percentage of pod set in common bean. The ones that already exist are relatively old and use cultivars and management systems different from those that currently occur (Ramalho and Ferreira, 1979; Izquierdo and Hosfield, 1981; Reis et al., 1985). Furthermore, common bean is grouped in some gene pools, the most important being the Andean and the Mesoamerican. No information is available on whether these gene pools affect the number of flowers and the percentage of a pod set. The common bean breeding program that has been carried out in the southern region of Minas Gerais has had attention on some characteristics besides grain yield. However, no reports were found on selection for N and V. It would be important, however, to verify if, during the decades of common bean selection in the region, there was some indirect effect for N and V. The effect of environment on expression of the two characters (N and V) has not yet been documented.
The knowledge of the number of flowers and percentage of pod set in a given condition, as already pointed out, is one of the alternatives to evaluate the yield potential of a plant/cultivar. For breeders, it would be important not only to evaluate the grain yield potential of lines but also to have information about the genetic control of these characters. No reports were found regarding genetic control of the number of flowers and the percentage of a pod set. In the study of genetic control, there are several methods in the literature (Bernardo, 2010; Hallauer et al., 2010; Ramalho et al., 2012). Among these methods, one of the most used is diallel crosses, mainly because of their versatility and type of information that is of great interest to breeders.
Therefore, the objective of this study was to obtain information about genetic control of the number of flowers and the percentage of pod set using diallel cross; to verify if the number of flowers and/or the percentage of pod set varies with environmental conditions and cultivar gene pool; to evaluate if the selection made over time indirectly affected the number of flowers and the percentage of pod set.
Materials and Methods
Local
The experiments were carried out at the Scientific and Technological Development Center of the Federal University of Lavras - UFLA, which is located at 919 m in altitude, 21°14’south latitude and 45°59’ west longitude.
Characteristics of parents used in diallel
Six lines from the UFLA Germplasm Bank were used, which were different in several traits, among them, the number of days for flowering, the gene pool, and the time of origin/ obtaining. Two Andean cultivars obtained before 1970 (Eriparsa and Goiano Precoce), both of type I growth habit and of the early cycle; and four Mesoamerican, two obtained before 1970 (Amarelinho and Paraná) and two after the year 2000 (Madrepérola and MAII-22), all of type III growth habit and normal cycle.
Obtaining the hybrid combinations
Diallel crosses involving six lines have been conducted, but no reciprocal ones. The crosses to obtain F1 generation were obtained under greenhouse conditions. To obtain hybrids, artificial hybridization technique was adopted (Antunes et al., 1980). Fifteen F1 hybrids obtained along with parents were seeded in the field to obtain F2 generation.
Evaluation of parents and segregant populations
The segregant populations were evaluated in F2, F3, and F4 generations along with the parents, with sowing in November, February, and July, respectively. The parents and the 15 hybrids were evaluated in a randomized complete block design, with four replications. The plots consisted of three 4-m rows with 15 seeds/m and then thinning was performed, leaving 10 plants/m. Crop management was as recommended for common bean crop in the region (Ramalho et al., 2014).
The aborted flowers were collected using a methodology similar to Izquierdo and Hosfield (1981). For this purpose, receptacles were constructed and placed in the central line of each plot (Figure 1A and B). This receptacle was 1.0 m in length, 0.50 m in width and 0.60 m in height. As a coating, a nylon U-shaped screen with 1 mm aperture was used. To make the receptacle, a wooden frame was made to support the nylon screen. At the lower end, it was cut. After germination, it was placed in the pot and in stages V3 and V4 of plants, the down part of the receptacle was sewn (Figure 1A).
The collects started about 10 days after flowering and were performed every 3 days. In each receptacle, all material was carefully collected to observe the presence of flowers containing ovary. The number of aborted flowers was obtained in each collection season.
At harvest, the following traits were obtained: - Number of pods per plant (X) - at the time of harvest, the number of pods inside the receptacle was recorded; - Number of total flowers (N) - obtained by the sum of the number of aborted flowers and the number of pods; - Percentage of pod set (V) - obtained by the estimator:
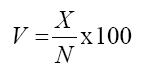
Grain yield (W) - individual plants were harvested and obtained grain yield per plant. Data were subjected to analysis of variance according to the model proposed by Steel et al. (1997). Analyses were carried out by generation/sowing season, considering genotype as fixed effect. To verify a possible effect of the collecting system used to obtain the aborted flowers, data from neighboring plants on the same line of receptacle were obtained. The same number of plants inside the receptacle was collected on contiguous line. Analysis of variance was performed for the number of pods (X) and grain yield (W). The analysis was subdivided into generations/time. Subsequently, we performed the joint analysis of the generations/time using the data obtained only inside the receptacle for N, V, and W.
Using the averages, the diallel analysis was performed, using Griffing (1956) method II, by the following model:

where yjmm’: hybrid combination average (m ≠ m’) or parent (m = m’) in the environment (j); μ: constant associated with all observations; gm: effect of general combining ability (GCA) of parent m (m = 1, 2, 3, ..., 6); smm’: effect of specific combining ability (SCA), between m and m’ parents; aj: effect of environment j (j = 1, 2, 3); (ga)jm: effect of GCA x environment interaction; (sa)jmm’: effect of SCA x environment interaction; ejmm’: experimental error associated with the mm’ hybrid combination, in environment j, the errors are independent and normally distributed with zero mean and with a common variance ejmm’ ∩ N (0, σ2).
The phenotypic correlations of characters two-to-two (rnv) were estimated, by season and in an average of seasons, using the estimator (Falconer and Mackay, 1996):
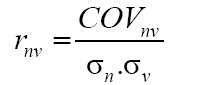
where COVnv: covariance between N (number of total flowers) and V (percentage of floral venation); σn: phenotypic deviation associated with N; σv: phenotypic deviation associated with V. Subsequently, the partial phenotypic correlations of the characters N, V, and W were estimated. For this purpose, the following estimator, proposed by Cruz et al. (2012), was used:
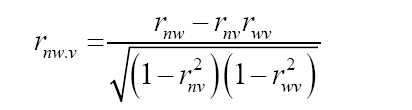
where rnw.v: partial phenotypic correlation between N and W, after removed the effects of V; rnw: phenotypic correlation between N and W; rnv: phenotypic correlation between N and V; rwv: phenotypic correlation between W and V.
The analyses were carried out with the statistical genetic Genes software (Cruz, 2013) and the MSTAT software (1991).
Results
The results obtained showed high and similar accuracies in each generation, all above 73.1%, indicating a good experimental precision, a condition that is indispensable for the accomplishment of the research (Table 1). The averages obtained for each trait in each generation and the corresponding means are presented in Table 1. The effect of the generations for most of the evaluated traits is evidenced. In most cases, the generation F2 was the one that always presented the highest averages.
| Characters | F2 | F3 | F4 | Mean | |||
| Mean | ├?┬?├?┬Łg | Mean | ├?┬?├?┬Łg | Mean | ├?┬?├?┬Łg | ||
| N | 40.35a | 82.95 | 27.53b | 84.75 | 27.98b | 78.45 | 31.95 |
| V | 43.96a | 77.38 | 40.34a | 86.24 | 36.83a | 91.27 | 40.38 |
| W | 14.43a | 78.68 | 10.68b | 85.23 | 8.93b | 83.31 | 11.35 |
*Means followed by the same letter in the line belong to the same group by the Scott-Knott test (1974).
Table 1: Mean and accuracy (├?┬?├?┬Łg) for the number of total flowers per plant (N), the percentage of pod set (V), and the grain yield per plant (W).
To verify the possible effect of the collecting system used to obtain the aborted flowers, analysis of variance was performed for the number of pods (X) and grain weight (W), considering the plants within the receptacle and those located in the same plot line, adjacent to the receptacle. It was observed (analysis not presented) in the joint analysis of the three generations that there was no significant difference for position effect (inside or outside the receptacle) and position x treatment interaction. Therefore, collecting system used did not affect the performance of plants and the information obtained can be generalized.
significant difference (P ≤ 0.05) was detected among treatments and also among generations for all the traits (Table 2). The interaction between treatments x generations was also significant, and it can be inferred that treatment response was not the same in the different generations. It can be inferred that the parents presented significant differences for all traits. The same occurred with the hybrid variation source. It was also found that generation x parent and generation x hybrid interactions were significant for most of the traits.
| FV | d.f. | N | V | W | ||||||
| SS | P | R2 | SS | P | R2 | SS | P | R2 (%) | ||
| Line/Generation | 9 | 74.73 | 0.00 | 83.86 | 0.00 | 28.03 | 0.00 | |||
| Treatments (T) | 20 | 334.06 | 0.00 | - | 308.07 | 0.00 | - | 56.13 | 0.00 | - |
| GCA | 5 | 407.65 | 0.00 | 30.5 | 735.72 | 0.00 | 59.7 | 163.41 | 0.00 | 72.78 |
| SCA | 15 | 309.52 | 0.00 | 69.5 | 165.51 | 0.00 | 40.3 | 20.38 | 0.01 | 27.22 |
| Generations (G) | 2 | 4449.97 | - | 1069.55 | - | 661.88 | ||||
| T x G | 40 | 114.54 | 0.00 | - | 64.53 | 0.00 | - | 14.72 | 0.22 | - |
| GCA x G | 10 | 184.23 | 0.00 | - | 98.88 | 0.00 | - | 25.17 | 0.00 | - |
| SCA x G | 30 | 91.32 | 0.13 | - | 53.09 | 0.19 | - | 11.23 | 0.32 | - |
| Average error | 180 | 59.53 | 38.22 | 9.68 | ||||||
| Mean | 31.96 | 40.38 | 11.35 | |||||||
R2: variation of the sum of squares (SS) of the treatments. d.f.: degrees of freedom.
Table 2: Summary of the joint diallel analysis for the number of total flowers per plant (N), the percentage of pod set (V), and the grain yield per plant (W) (g/plant).
It was observed that the Paraná genitor was the one that most stood out in the average of the three generations for N (Table 3). Goiano Precoce line presented the smaller N among the parents. In the average of the three generations, the hybrids produced 22.90% more flowers than the parents (Table 4). This result evidenced the occurrence of a significant mean heterosis for the number of flowers per plant. For the percentage of pod set, the parents of Mesoamerican gene pool (Madrepérola, Paraná, Amarelinho, and MAII-22) presented the higher averages of the three generations. For N, mean of hybrids was 5% lower than the average of parents, also evidencing the occurrence of medium heterosis, but reducing the expression of the character. For grain yield per plant (W), in an average of the three generations, the parents Madrepérola, Paraná, and MAII-22 were the most productive ones, and the other ones were classified in the same group. For W, only the hybrid Paraná x Amarelinho, Paraná x MAII-22, MAII-22 x Madrepérola, and MAII-22 x Eriparsa combinations were in the group of larger W.
| Parents | N | V | W |
| Madrepérola | 27.61b | 46.39a | 14.69a |
| Paraná | 35.76a | 48.45a | 14.11a |
| Eriparsa | 26.36b | 31.65b | 8.65b |
| Amarelinho | 28.04b | 43.66a | 8.57b |
| Goiano Precoce | 20.70b | 35.82b | 8.38b |
| MAII-22 | 26.32b | 45.18a | 12.76a |
| Paraná x Amarelinho | 31.23b | 49.48a | 12.88a |
| Paraná x Goiano Precoce | 41.69a | 38.43b | 11.06b |
| Paraná x Eriparsa | 39.18a | 38.84b | 11.06b |
| Paraná x MAII-22 | 37.68a | 42.22a | 14.67a |
| Paraná x Madrepérola | 33.61a | 35.68b | 10.46b |
| Goiano Precoce x Eriparsa | 24.18b | 35.76b | 9.58b |
| Goiano Precoce x MAII-22 | 35.04a | 35.88b | 10.37b |
| Goiano Precoce x Amarelinho | 35.62a | 33.33b | 8.76b |
| Goiano Precoce x Madrepérola | 29.59b | 36.21b | 9.56b |
| MAII-22 x Amarelinho | 30.61b | 43.35a | 11.51b |
| MAII-22 x Madrepérola | 34.36a | 42.06a | 15.78a |
| MAII-22 x Eriparsa | 35.81a | 42.23a | 12.11a |
| Madrepérola x Amarelinho | 28.70b | 45.94a | 11.31b |
| Madrepérola x Eriparsa | 34.05a | 40.51a | 11.39b |
| Eriparsa x Amarelinho | 34.94a | 36.89b | 10.65b |
*Means followed by the same letter in the column belong to the same group by the Scott-Knott test (1974).
Table 3: Mean of the total number of flowers per plant (N), the percentage of pod set (V), and the grain yield per plant (W).
| Characters | Treatment | Generations | |||
| F2 | F3 | F4 | Mean | ||
| N | Parents | 33.79 | 24.48 | 24.12 | 27.46 |
| Hybrid | 42.98 | 28.75 | 29.53 | 33.75 | |
| Mean [h (%)] | 27.20 | 17.44 | 22.42 | 22.91 | |
| V | Parents | 45.76 | 41.88 | 37.94 | 41.86 |
| Hybrid | 43.25 | 39.73 | 36.39 | 39.79 | |
| Mean [h (%)] | -5.49 | -5.13 | -4.08 | -4.95 | |
| W | Parents | 14.25 | 10.64 | 8.70 | 11.19 |
| Hybrid | 14.50 | 10.69 | 9.03 | 11.41 | |
| Mean [h (%)] | 1.75 | 0.47 | 3.79 | 2.79 | |
Table 4: Estimation of mean heterosis in percentage for the number of total flowers (N), the percentage of pod set (V), and the grain yield per plant (W).
In a diallel analysis of three generations, it was found a significant difference (P ≤ 0.01) in GCA and for SCA for N (Table 2). In the interactions, only GCA x generations were significant (P ≤ 0.01). The sum of squares of treatments explained by GCA (R2) was lower than the SCA, explaining only 30.5% of total variation of the treatments. These lower values of R2 indicated that dominance effect in control of the N trait occurred, as already mentioned.
GCA (gi) estimates for N are presented in Table 5. As expected, Paraná genitor, which obtained the highest mean for N, presented the highest gi estimation; therefore, it contributed to improving the expression of character in hybrid combinations. The opposite, as was expected, occurred with “Goiano Precoce”. In GCA estimates, interaction with generations is again well evidenced. However, in all cases, the “Paraná” always presented estimates of positive GCA.
| Parents | Mean | ||
| N | V | W | |
| Paraná | 3.90 | 2.36 | 1.11 |
| Eriparsa | -0.35 | -3.14 | -0.92 |
| Amarelinho | -0.81 | 1.71 | -0.89 |
| Goiano Precoce | -2.02 | -3.93 | -1.67 |
| MAII-22 | 0.30 | 1.68 | 1.32 |
| Madrepérola | -1.02 | 1.32 | 1.05 |
| SD (Gi) | 1.19 | 0.98 | 0.48 |
| SD (Gi - Gj) | 1.84 | 1.52 | 0.75 |
Table 5: Estimates of the general combining ability (GCA) for the number of flowers (N), the percentage of pod set (V), and the grain yield per plant (W).
Results for SCA were consistent with the mean test performed (Tables 3 and 6). In all cases, the hybrid combinations that were in the group of the highest number of flowers per plant also had high and positive SCA values.
| Parents/Hybrids | |||
| N | V | W | |
| Paraná | -4.00 | 3.35 | 0.53 |
| Eriparsa | -4.90 | -2.45 | -0.86 |
| Amarelinho | -2.29 | -0.13 | -0.98 |
| Goiano Precoce | -7.21 | 3.30 | 0.37 |
| Maii-22 | -6.25 | 1.44 | -1.22 |
| Madreperola | -2.30 | 3.38 | 1.23 |
| Paraná x Amarelinho | -3.81 | 5.04 | 1.32 |
| Paraná x Goiano Precoce | 7.85 | -0.39 | 0.27 |
| Paraná x Eriparsa | 3.67 | -0.76 | -0.49 |
| Paraná x MAII-22 | 1.52 | -2.20 | 0.89 |
| Paraná x Madrepérola | -1.23 | -8.38 | -3.06 |
| Goiano Precoce x Eriparsa | -5.41 | 2.45 | 0.82 |
| Goiano Precoce x MAII-22 | 4.80 | -2.26 | -0.63 |
| Goiano Precoce x Amarelinho | 6.50 | -4.83 | -0.03 |
| Goiano Precoce x Madrepérola | 0.68 | -1.56 | -1.17 |
| MAII-22 x Amarelinho | -0.84 | -0.42 | -0.26 |
| MAII-22 x Madrepérola | 3.12 | -1.31 | 2.06 |
| MAII-22 x Eriparsa | 3.90 | 3.31 | 0.36 |
| Madrepérola x Amarelinho | -1.42 | 2.54 | -0.20 |
| Madrepérola x Eriparsa | 3.47 | 1.96 | -0.10 |
| Eriparsa x Amarelinho | 4.15 | -2.06 | 1.12 |
| SD (Sii) | 2.70 | 2.23 | 1.10 |
| SD (Sij) | 3.27 | 2.70 | 1.32 |
| SD (Sii - Sjj) | 3.68 | 3.05 | 1.19 |
| SD (Sij - Sik) | 4.88 | 4.03 | 1.98 |
| SD (Sij - Skl) | 4.51 | 3.73 | 1.83 |
Table 6: Estimates (SCA) in the mean of environments for the number of flowers (N), the percentage of pod set (V), and the grain yield per plant (W) (g/plant).
For the percentage of pod set (V), there was the effect on both GCA and SCA in diallel analysis involving the three generations (Table 2). The GCA sum of squares was higher than that of the SCA, explaining 59.7% of this variation. It can be inferred that there are additive and dominance effects in control of the percentage of the pod set.
The results of GCA for V were similar to those of N (Table 5). Again, the parents with higher V averages (Paraná, Amarelinho, MAII-22, and Madrepérola) presented the highest GCA estimates (gi). This result shows that these parents present a higher average performance in hybrid combinations. Estimates of SCA are presented in Table 6. The Paraná x Amarelinho cross was the one that presented the highest estimate of SCA (5.04). It is worth mentioning that these two parents were the ones that also presented higher gi. Unlike what was seen for the N, the SCA estimates were not consistent with the mean values obtained for each hybrid combination. In this case, the combinations of higher mean values for V were not always high and positive.
The diallel analysis for the three generations for grain weight (W) is shown in Table 2. There was an effect of both GCA and SCA (P < 0.01). The GCA sum of squares was always higher than that of SCA, explaining about 72.78% for W, and therefore, can be inferred that there is a predominance of the additive effect in its genetic control. The estimates of the GCA (gi) for W are shown in Table 5. It can be seen that the parents Paraná, MAII-22, and Madrepérola presented higher estimates of gi, and also presented higher averages for W, as already mentioned. Estimates of the SCA again coincide with the mean values of the hybrid combinations. In the majority, combinations that presented higher W were the ones that had the highest SCA estimation (Table 6).
The estimates of the correlations between N, V, and W are presented in Table 7. As expected, estimates between N or V with W were always positive. However, the correlations between N and V were, in most cases, negative. Therefore, part of the correlation between N with W or V with W is influenced by the effect of the negative association of N and V. Then, partial correlations of N with W were estimated, disregarding the effect of V, and V with W, disregarding the N effect. In all cases, correlations were always positive, as previously reported. However, the magnitude of partial correlations was higher concerning the correlations presented in Table 7, in most cases.
| Characters | F2 | F3 | F4 | Mean |
| N x W | 0.40 | 0.30 | 0.57** | 0.33 |
| N x V | -0.54* | -0.60* | 0.01 | -0.29 |
| V x W | 0.38 | 0.68** | 0.58** | 0.70** |
| Partial phenotypic correlation (N), (V), and (W) | ||||
| N x W | 0.59* | 0.62* | 0.48 | 0.43 |
| V x W | 0.57* | 0.79* | 0.50 | 0.72** |
**,*Significant (P < 0.01 and P < 0.05, respectively) by the F-test.
Table 7: Estimates of simple phenotypic correlation for the number of total flowers (N), the percentage of pod set (V), and the grain yield per plant (W).
Discussion
The number of pods per plant (X) in common bean is one of the most important components for initial yield, as already mentioned (Costa and Zimmermann, 1988; Zilio et al., 2011; Guilherme et al., 2014). The number of pods depends on the number of flowers produced (N) and the percentage of pod set (V). Thus, to have information about yield potential of a plant, one must have information of N and V. However, these two traits are difficult to measure, so it has little information on this.
One of the first studies on the number of flowers was carried out in the United States (Smith and Pryor, 1962). Later, Ramalho and Ferreira (1979) carried out a similar study with Brazilian cultivars. To estimate the N, each flower was identified by a worsted yarn when emerged. The difficulty of marking is enormous and of dubious accuracy because in the same inflorescence can occur several flowers that open at different times. Besides, the consistent handling of flowers should affect the percentage of the pod set.
In this study, aiming to estimate V Izquierdo and Hosfield (1981) proposed the use of a specific receptacle. In that case, the aborted flowers fall into the receptacle being counted periodically. Subsequently, in harvest, the number of pods is obtained. Adding some pods to aborted flowers, a total number of flowers can be obtained. Reis et al. (1985) working with a common bean in intercropping with maize in Brazil, also used this process to obtain estimates of some flower and percentage of a pod set; this was the procedure used in the present study.
However, it could be argued that receptacle and handling it to collect fallen flowers could reduce floral venation, and therefore, provide an unreliable estimate. To prove this fact or not, in this study, at the time of harvest, the pods were collected inside the receptacle and also on the same contiguous line. It was found that there was no significant difference in the number of pods and that the interaction lines and hybrids x positions (inside or outside the receptacle) were not significant at the evaluation times. It will be understood that receptacle did not interfere with N or V.
The objective was to evaluate the generations in different seasons of sowing, to have results that could be generalized. The experiments were done in regular growing seasons in the southern region of Minas Gerais State. Seeds were sown in November, February, and July. These sowing seasons have a wide variation in temperature and precipitation conditions (Ramalho et al., 2014). Also, in every season, a different generation of diallel populations was evaluated. Thus, the effect of generations and sowing season could not be individualized. It was verified that there was an effect of sowing season/generation (Table 1). For almost all traits, the highest overall mean was obtained in an F2 generation, sown in November. At this season, temperature and precipitation were higher, which may have contributed to the better performance of common bean. However, the F2 generation also has more heterozygosity than F3 and F4, and it is expected that the average of this generation will be higher if dominance occurs (Ramalho et al., 2012).
Interaction treatments (parents and hybrids) x generations/seasons were significant, and it was possible to infer that behaviors of parents and hybrids were not coincident between generations/seasons. In common bean, several studies report an interaction of genotype x sowing season, especially for grain yield (Lima et al., 2014; Ferreira et al., 2015). There are also reports of the genotype x environment interaction for other traits of common bean, including some pods per plant, grain per pod, and grain weight (Ribeiro et al., 2014). Although an interaction has occurred, the most significant results were concordant between generations/ seasons, and for this reason, emphasis on discussion of results will be directed to what occurred in the average of three generations.
It is difficult to obtain N and V per plant, as already mentioned. However, only obtaining the data for some lines is not enough, it is necessary to have information about the genetic control. There are some methodologies to reach this goal (Hallauer et al., 2010; Ramalho et al., 2012). Among them, the diallel crosses stand out. The success of the diallel crosses depends, in a first instance, on the careful choice of the parents. In this study, parents/ lines were chosen that represent different times of achievement and also belong to different gene pools. Among the Mesoamerican parents, two were widely used in the past Amarelinho and Paraná. However, Madrepérola is a cultivar currently recommended for cultivation in Minas Gerais (Carneiro et al., 2012) and MAII-22 is a line recently obtained in recurrent selection program aiming to resistance to an angular spot of common bean. Andean cultivars have determined growth habit and big grains. Mesoamerican has indeterminate growth habit, type III, and medium grain. Thus, we used parents with wide variation in traits of importance in common bean breeding program.
As discussed earlier, the number of pods is dependent on the number of total flowers (N) that a plant produces. The average N was 31.9 flowers per plant (Table 1). The Paraná genitor presented the highest average estimate of the three generations, 35.8 flowers (Table 3). This line was obtained before the 1970s and can infer that selection of lines performed in the last 40 years did not contribute to increasing the number of flowers. In general, Andean cultivars always presented relatively low N, especially genitor Goiano Precoce, with only 20.7 flowers in an average of the three generations (Table 3). This fact can be explained because the time of flowering of Andean lines is lower than of the Mesoamerican lines and the growth habit is determined.
In genetic control of N, SCA explained the highest proportion of the sum of squares of treatment (R2 = 69.5%), indicating dominance in control of this trait (Table 2). This fact can be verified by the superiority of average hybrids, which was 22.9% higher than the average of parents (Table 4). Reports on the genetic control of the number of flowers in common bean were not found. However, in soybean, loci with dominant allelic interaction in the genetic control of N have been related, as verified in the present study (Van Schaik and Probst, 1958).
Another trait that influences the number of pods is the percentage of pod set (V). In average, V was 40.4%, i.e., only 40.4% of flowers produced pods. Usually, the percentage of pod set is small. Reports in the literature indicate lower values than those obtained in this study. Similar results to this study were found by Izquierdo and Hosfield (1981) when studying flower abscission in common bean. However, Ramalho and Ferreira (1979), in a study involving five bean cultivars found the percentage of pod set of 28%. Probably this discrepancy may be due to the methodology used by Ramalho and Ferreira (1979), where each flower was marked by a wool yarn, which, as already mentioned, may have affected the percentage of the pod set. These results show that the plant does not express its full potential; this is related to several reasons, like edaphoclimatic factors, as already demonstrated for the common bean (Fancelli, 2009; Zilio et al., 2011).
In mean of three generations, cultivars of the Mesoamerican gene pool presented higher values of V (Table 3). It can be inferred that V depends on the gene pool, i.e., depends on the cultivar origin. It is also inferred that Mesoamerican genotypes, except Paraná, although have obtained a higher V, were classified in the group of smaller N. It is verified that, while for N the heterosis increases the expression of character, for V, the heterosis reduces. For V, mean heterosis estimate was negative (-4.95%), indicating that if dominance occurs, it is reducing expression of character.
Estimate of the sum of squares explained by GCA and SCA for V confirms that heterosis is smaller than that of N since R2 of GCA (59.7%) was slightly higher than that of SCA (Table 2). No report in this respect was found in the literature. Mesoamerican parents presented the highest estimates of GCA (gi). High gi values (positive or negative) indicate better performance in hybrid combinations. Therefore, lines with high GCA contribute to the greater expression of character in crosses. In the diallel analysis of V, GCA estimates were well consistent with parent mean, which was already expected (Tables 3 and 5). In studies performed by Oliveira et al. (1996), evaluating flowering and grain yield, it was observed that when there is a predominance of additive effects in control of the characters, there is good agreement between average performance of parents and GCA estimate; this corroborates with comments made previously in the present study.
For grain yield (W) both GCA and SCA were significant. However, the GCA sum of squares was always higher than that of the SCA, which explained 72.78% of the total variation of treatments (Table 2). W of parents on average was very similar to that found in hybrids, 11.19 g/plant for parents and 11.41 g/plant for hybrids (Table 4). In this case, the dominance effect is small. As the parents are genotypically different for W, it can be inferred that the expression of character was predominantly dependent on loci with additive alleles. Reports found in the literature differ on genetic control of this character. Several studies have reported the presence of genes with an additive effect, similar to those found in the present study (Takeda et al., 1991; Vizgarra et al., 1992; Silva et al., 2004; Moreto et al., 2007). However, there are reports that occurrence of dominance was also important in W (Chung and Stevenson, 1973; Foolad and Bassiri, 1983; Guilherme et al., 2014).
Partial correlations of N with W, fixing effect of V, or of V with W, and fixing effect of N were always positive (Table 7). In other words, as expected, both the number of flowers and percentage of pod set affect grain yield positively. However, the correlation between N and V was always negative. In an average of the three generations rnv = -0.29. It is inferred that plants with a greater number of flowers tend to have less percentage of the pod set. This fact has also been verified for correlations of the three primary components of grain yield of bean (X, Y, and Z) with W (Lima and Ramalho, 2016). The relative contribution of X, Y, and Z varies according to environmental conditions, as occurred in this study. Lima and Ramalho (2016) discuss this question from the perspective of geometry. According to these authors, grain yield (W) is as if it were a parallelepiped, in which products of the axes X, Y, and Z would be equal to W. Since the largest volume of the parallelepiped is the cube, the contribution of X, Y, and Z would have to be the same to obtain the maximum W.
Extrapolating to the case of N and V, one could infer that the ideal would be to have a condition in which the relative contribution of N and V to W was similar. In reality, there is no independence between N and V, i.e., for a given environmental condition, if one plant produces many flowers, surely its percentage of pod set will be less than another plant that produces fewer flowers, where N will be smaller. This fact may explain why the grain yield of the Andean parents with the Mesoamerican is usually lower. In Andean cultivars, as already commented, N is smaller than Mesoamerican cultivars and usually also the percentage of pod set is smaller, as was observed in this study. However, within the same gene pool, N and V act as a stability factor of grain yield, which means that when the environmental condition is favorable for flowering and unfavorable for grain filling, N is larger and V smaller. If the opposite occurs, N will be smaller, and V will be larger. The ideal would be the favorable environmental condition in both flowering and grain filling. In this case, the larger N and V would contribute with similar proportions for grain yield. When selecting for grain yield, as the breeders usually do, are indirectly selecting for a better N and V equilibrium according to the environmental condition.
Conclusion
The number of flowers of common bean is on average 31.9, and the percentage of pod set is 40.4%. The average of Mesoamerican parents, in general, for N and V is higher than in the Andean. The selection made by breeders over the time does not contribute to increasing N and V.
The SCA explained most of the variation in the number of total flowers, evidencing predominance of dominance effect to increase the expression of character in its genetic control. However, for the percentage of pod set, dominance contribution was slightly lower than the GCA and aimed at character reduction, which indicates that for genetic control of V, dominant and additive loci occur.
The parents differed in the GCA (gi) estimate for N and V. Lines of Mesoamerican origin always presented estimates of CGC positive for V.
The higher the number of total flowers, the smaller the percentage of a pod set. The greater the percentage of a pod set or the greater the number of flowers, the greater the grain yield. These two traits are very influenced by environment and should act as a strategy for greater stability of the common bean grain yield.
Acknowledgments
We thank Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) and the National Council for Scientific and Technological Development (CNPq) for the scholarship granted.
About the Authors
Corresponding Author
E.S. Martins
Departamento de Gen├â┬ętica, Escola Superior de Agricultura ├óÔéČ┼ôLuiz de Queiroz├óÔéČ┬Ł, Universidade de S├â┬úo Paulo, S├â┬úo Paulo, SP, Brasil
- Email:
- emanoelmartins92@hotmail.com
References
- Antunes IF, Teixeira MO and Zimmermann MJ (1980). Maximização da eficiência de cruzamentos artificiais em feijão (Phaseolus vulgaris L.). Embrapa Arroz e Feijão, Goiânia.
- Bernardo R (2010). Breeding for quantitative traits in plants. 2nd edn. Stemma, Woodbury.
- Carneiro JES, Abreu AFB, Ramalho MAP, Paula Júnior TJ, et al. (2012). BRSMG Madrepérola: common bean cultivar with late-darkening Carioca grain. Crop Breed. Appl. Biotechnol. 12: 281-284. https://doi.org/10.1590/S1984-70332012000400008
- Chung JH and Stevenson E (1973). Diallel analyses of the genetic variation in some quantitative characters in dry beans. N. Z. J. Agric. Res. 16: 223-231.https://doi.org/10.1080/00288233.1973.10421139
- Costa JCG and Zimmermann MJO (1988). Melhoramento genético. In: A cultura do feijoeiro: fatores que afetam a produtividade (Zimmermann MJO, Rocha M and Yamada T eds.). Potafós, Piracicaba, 229-245.
- Cruz CD (2013). GENES - a software package for analysis in experimental statistics and quantitative genetics. Acta Scient. 35: 271-276.
- Cruz CD, Regazzi AJ and Carneiro PCS (2012). Modelos biométricos aplicados ao melhoramento genético. 4th edn. UFV, Viçosa.
- Falconer DS and Mackay TFC (1996). Introduction to quantitative genetics. 4th edn. Longman Group Limited, Edinburgh.
- Fancelli AL (2009). Feijão: Tópicos Especiais de Manejo. ESALQ/USP/LPV, Piracicaba.
- Ferreira RAC, Ramalho MAP, Toledo FHRB and Abreu AFB (2015). Implications of the number of years assessment on recommendation of common bean cultivars. Plant Breed. 134: 599-604. https://doi.org/10.1111/pbr.12302
- Foolad MR and Bassiri A (1983). Estimates of combining ability, reciprocal effects and heterosis for yield and yield components in a common bean diallel cross. J. Agric. Sci. 100: 103-108. https://doi.org/10.1017/S0021859600032482 Griffing BA (1956). Generalized treatment of the use of dialiel crosses in quantitative inheritance. Her. 10: 31-50. https:// doi.org/10.1038/hdy.1956.2
- Guilherme SR, Ramalho MAP, de F B Abreu A and Pereira LA (2014). Genetic control of inflorescence in common bean. Genet. Mol. Res. 13: 10349-10358.PubMed https://doi.org/10.4238/2014.December.4.30
- Hallauer AR, Miranda Filho JB and Carena MJ (2010). Quantitative genetics in maize breeding. Springer, New York. Izquierdo J and Hosfield GL (1981). A collection receptacle for field abscission studies in common beans (Phaseolus vulgaris L.). Crop Sci. 21: 622-625.https://doi.org/10.2135/cropsci1981.0011183X002100040035x
- Lima JG and Ramalho MAP (2016). Geometry applied to breeding commom beans (Phaseolus vulgaris L.). Genet. Mol. Res. 15: 1-7.https://doi.org/10.4238/gmr.15027873
- Lima LK, Ramalho MAP, Abreu AFB, Toledo FHRB, et al. (2014). Implications of predictable and unpredictable environmental factors in common bean VCU triais in Minas Gerais. Crop Breed. Appl. Biotechnol. 14: 146-153. https://doi.org/10.1590/1984-70332014v14n3a22
- Moreto AL, Ramalho MAP, Nunes JAR and Abreu AFB (2007). Estimação dos componentes da variância fenotípica em feijoeiro utilizando método genealógico. Cienc. Agrotec. 31: 1035-1042. https://doi.org/10.1590/S1413-70542007000400014
- Oliveira LB, Ramalho MAP, Abreu AFB and Ferreira DF (1996). Alternative procedures for parent choice in a breeding programm for the common bean (Phaseolus vulgaris L.). Genet. Mol. Biol. 19: 611-615.
- Ramalho MAP and Ferreira MM (1979). Comportamento de cultivares de feijão (Phaseolus vulgaris L.) em relação ao florescimento e vingamento das vagens. Ciênc. Prát. 3: 80-83.
- Ramalho MAP, Abreu AFB, Guilherme SR (2014). Informações técnicas para o cultivo do feijoeiro-comum na região Central-Brasileira. FUNDECC, Lavras.
- Ramalho MAP, Abreu AFB, Santos JB and Nunes JAR (2012). Aplicações da Genética Quantitativa no Melhoramento de Plantas Autógamas. UFLA, Lavras.
- Reis WP, Ramalho MAP and Cruz JC (1985). Arranjos e populações do feijoeiro na consorciação com o milho. Pesqui. Agropecu. Bras. 20: 575-584.
- Ribeiro ND, Domingues LS and Zemolin AEM (2014). Avaliação dos componentes da produtividade de grãos em feijão de grãos especiais. Cient. 42: 178-186. https://doi.org/10.15361/1984-5529.2014v42n2p178-186
- Silva MP, Júnior ATA and Rodrigues R (2004). Análise dialélica da capacidade combinatória cru feijão-de- vagem. Hortic. Bras. 22: 277-280.https://doi.org/10.1590/S0102-05362004000200022
- Smith FL and Pryor RH (1962). Effects of maximum temperature and age of flowering and seed production in there bean variets. Hilg. 33: 669-687. https://doi.org/10.3733/hilg.v33n12p669
- Steel RGD, Torrie JH and Dickey DA (1997). Principles and procedures of statistics: a biometrical approach. McGraw-Hill, New York.
- Takeda C, Santos JB and Ramalho MAP (1991). Progeny test for the ESAL 501 x A354 common bean (Phaseolus vulgaris L.) hybrid at different locations. Braz. J. Genet. 14: 771-779.
- Van Schaik PH and Probst AH (1958). Effects of some environmental factors on flower production and reproductive efficiency in soybeans. Agron. J. 50: 192-197. https://doi.org/10.2134/agronj1958.00021962005000040007x
- Vizgarra ON, Morales FJ and Ramalho MAP (1992). Combining abilities of some common bean (Phaseolus Vulgaris L.) cultivars having mechanisms of resistance to bean golden mosaic virus (BGMV). Brazil. J. Genet. 15: 871-878.
- Zilio M, Coelho CMM, Souza CA, Santos JCP, et al. (2011). Contribuição dos componentes de rendimento na produtividade de genótipos crioulos de feijão (Phaseolus vulgaris L.). Rev. Cienc. Agron. 42: 429-438. https://doi.org/10.1590/ S1806-66902011000200024
Keywords:
Download:
Full PDF- Share This
