Environmental stratifications for soybean cultivar recommendation and its consistency over time
Published: July 06, 2017
Genet.Mol.Res. 16(3): gmr16039693
DOI: 10.4238/gmr16039693
Abstract
Stratification of environments is a strategy to capitalize genotype x environment (GxE) interaction, which can optimize the process of assessment and cultivar recommendation, increasing productivity in a target environmental population. The objective of this study was to assess environmental stratification methods based on the analysis of GxE interaction, to identify consistent agronomic zones across time for soybean. Grain yield data of inbred lines from three maturity groups (early, medium, and late) were used. Lines and cultivars were tested in regional variety trials during three growing seasons at eighteen locations in the tropics of Central Brazil. Three methods were applied to stratify the environments. The first was based on joint analyses of variance for all the pairs of locations within each growing year. The second was based on a distance measure between each pair of locations, which was related to the GxE interaction estimated via additive main effects and multiplicative interaction analysis. The third was based on the approach of winning genotypes. The stratification results from the first two methods were not consistent across the growing seasons. However, the winning genotype approach provided consistent environmental stratification across years. From locations used in the genotypic assessment, three environmental clusters were identified for the early and medium maturity groups of soybean, and four clusters for the late maturity group. The use of different genotypic sets across years reinforces the predictive value of the environmental stratification established.
Introduction
Regional cultivar assessment trials are usually carried out in several locations under heterogeneous environmental conditions with a large number of genotypes. In this situation, the selection and recommendation are complicated by the interaction of the different genotypes with the heterogeneous environments, a phenomenon known as GxE interaction. The maximization of the yield in a region where this interaction is high has been associated with the possibility of stratifying this region; that is, subdividing it into relatively homogeneous zones (environmental strata) and recommending high-yielding genotypes for each zone.
One of the oldest methods for environmental stratification was developed by Horner and Frey (1957). In this method, the locations are grouped according to the similarity of their interactions with the tested genotypes. A disadvantage of this method is that clustering does not offer information about the performance of genotypes in the assessed environments. According to Romagosa and Fox (1993), this problem can be overcome by using a method based on models of additive main effects and multiplicative interaction-AMMI analysis. This method integrates traditional analysis of variance for the main effects (genotypes and environments) with the principal component analysis (PCA) for the interaction effects between these factors. Gauch and Zobel (1997) proposed an approach based on AMMI analysis that performs the stratification of environments, identifying, at the same time, genotypes adapted specifically to each stratum. In this approach, called “winning genotype methodology”, the strata are defined by the genotypes with the highest yield in each environment (winner genotypes). These genotypes have specific adaptation and agronomic stability to the environmental stratum that they determine.
The GxE interaction may lead to overestimations of the heritability value, with consequent overestimation of the gains to be achieved with the selection. It may also imply in a reduction in the overall productivity of an area for which a general recommendation of a given cultivar is made. On the other hand, one can take advantage of its existence using statistical procedures that identify the pattern of this interaction, generating information that allows the grouping of sites in strata within which the magnitude of the interaction is not significant. Specific recommendations for such strata would maximize the production of the whole region under consideration. Likewise, the conduct of the selection programs considering such zoning would provide more accurate estimates of the selection gains.
This paper reports the assessment of three environmental stratification methods, performed by GxE interaction analyses of multi-environment variety trials in soybean. From this, it was aimed to identify a method that provides more consistent agronomic zones over time, and, as a consequence, a stratification of mega-environments for soybean cultivar recommendation in the tropics of Central Brazil. Soybeans are grown in extensive areas of this country, mainly in the region of Brazilian savannah (Cerrado).
Materials and Methods
Grain yield (kg/ha) data from regional trials of soybean inbred lines of three maturity groups (early, medium and late) from different growing seasons (1999/2000, 2000/2001, and 2001/2002) were used. The trials were carried out at eighteen locations of the central region of Brazil (Table 1), with a predominance of areas with Latosol soils (like Oxisols in U.S. Soil Taxonomy) in the Brazilian savannah region.
| State | Municipality (site) | Code1 | Latitude South | Longitude West | Altitude (m) |
| GO | Anápolis | ANAP | 16°27' | 48°57' | 1017 |
| GO | Chapadão do Céu | CCEU | 18°32' | 52°32' | 800 |
| GO | Cristalina | CRIS | 16°50' | 47°36' | 930 |
| GO | Luziânia | LUZI | 16°16' | 47°57' | 930 |
| GO | Mineiros | MINE | 17°34' | 52°33' | 980 |
| GO | Rio Verde | RVER | 17°41' | 50°55' | 730 |
| GO | Senador Canedo | SCAN | 16°33' | 49°05' | 801 |
| BA | Correntina | CORR | 13°33' | 44°38' | 950 |
| BA | Placas | PLAC | 11°08' | 47°38' | 780 |
| DF | Pamplona | PAMP | 16°05' | 47°30' | 1008 |
| DF | Planaltina | PLAN | 15°31' | 47°36' | 1003 |
| MG | Buritis | BURI | 15°27' | 46°25' | 900 |
| MG | Capinópolis | CAPI | 18°41' | 49°34' | 950 |
| MG | Conquista | CONQ2 | 19°52' | 47°32' | 830 |
| MG | Iraí de Minas | IRAI | 18°57' | 47°27' | 975 |
| MG | Sacramento | SACR | 19°51' | 47°26' | 1038 |
| MG | Uberaba | UBBA | 19°42' | 47°55' | 781 |
| MG | Uberlândia | UBRL2 | 19°05' | 48°16' | 1012 |
| MT | Lucas do Rio Verde | LVRE | 13°09' | 55°54' | 350 |
1These codes are also used to identify these locations in the figures of this paper. 2CONQ was included only in the late maturity group trials, and UBRL was not included in this maturity group.
Table 1: Locations and their geographic coordinates, where the variety trials of inbred soybean lines were carried out in tropics of Central Brazil.
A randomized complete block design with four replications was used in each trial. The treatments consisted of experimental inbred lines and checked cultivars, which were different in the different years; this is a positive aspect for the inferences because the cultivated soybean germplasm is better represented. The number of treatments in each growing season and maturity group ranged from 23 to 28. The plots consisted of four 5.0 m rows, spaced 0.5 m apart. The useful area of the plot consisted of the two central rows, and 0.5 m was discarded from each end.
First, analyses of variance (ANOVA) were performed for each experiment, that is, for each maturity group, location, and growing season. Joint ANOVA were then carried out, including all locations for each maturity group in each crop year. Finally, joint analyses were made for each pair of locations in each maturity group and growing season. The homogeneity test of the error mean squares was performed by comparing the minimum and maximum values according to Hartley (1950).
The GxE interaction sums of squares obtained from the joint analyses were partitioned via AMMI analysis. In this model, the phenotypic response of a genotype in a given environment (Yij) is expressed similarly to the classical joint analysis model; however, the original term (ge)ij, that describes the interaction of ith genotype (I = 1, 2, ..., g) with jth environment (j = 1, 2, ..., e), is modeled as  Its first part with multiplicative components is called pattern, and corresponds to the GxE interaction itself, according to this approach. The other part (ρij) is referred as noise in the original interaction term. Thus, the complete model is
Its first part with multiplicative components is called pattern, and corresponds to the GxE interaction itself, according to this approach. The other part (ρij) is referred as noise in the original interaction term. Thus, the complete model is 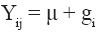
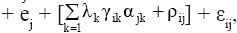 where μ is a constant common to the Yij responses, i.e., the general mean of the experiment; gi is the effect of ith genotype (here considered as random effect because they represent a sample of the population of genotypes evaluated annually in multi-environment trials); ej is the effect of jth environment (assumed as fixed effect); λk is the kth singular value of the interaction matrix, defined as
where μ is a constant common to the Yij responses, i.e., the general mean of the experiment; gi is the effect of ith genotype (here considered as random effect because they represent a sample of the population of genotypes evaluated annually in multi-environment trials); ej is the effect of jth environment (assumed as fixed effect); λk is the kth singular value of the interaction matrix, defined as 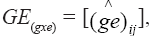 where
where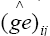 is the random effect of the interaction between genotype gi and environment ej. The value λk (k = 1, 2, ..., p; where “p” is the rank of the GE matrix), expressed in the same units as Yij, is related to a partition of the GE sum of squares,
is the random effect of the interaction between genotype gi and environment ej. The value λk (k = 1, 2, ..., p; where “p” is the rank of the GE matrix), expressed in the same units as Yij, is related to a partition of the GE sum of squares, 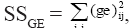 in “p” decreasing components, where the first “n” components (n<p) describe the systematic part (pattern) in the SSGE, and the other “p-n” expresses the random part (noise), which is described by ρij; γik is a non-dimensional effect, the ith element of the (GE)(GE)’ eigenvector associated with λk that represents the weight of the ith genotype in the kth portion of the SQGE; αjk is also a non-dimensional effect, the jth element of the (GE)’(GE) eigenvector associated with λk that represents the weight of jth environment in the kth portion of the SQGE; and
in “p” decreasing components, where the first “n” components (n<p) describe the systematic part (pattern) in the SSGE, and the other “p-n” expresses the random part (noise), which is described by ρij; γik is a non-dimensional effect, the ith element of the (GE)(GE)’ eigenvector associated with λk that represents the weight of the ith genotype in the kth portion of the SQGE; αjk is also a non-dimensional effect, the jth element of the (GE)’(GE) eigenvector associated with λk that represents the weight of jth environment in the kth portion of the SQGE; and 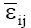 is the mean experimental error, assumed to be independent and with a normal distribution, zero mean, and common variance.
is the mean experimental error, assumed to be independent and with a normal distribution, zero mean, and common variance.
The model was adjusted sequentially, combining ANOVA and PCA. The residuals from the fitting of main effects by ANOVA 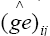 are arranged in the GE matrix and fitted in the second step via PCA. This analysis must be performed in a integrated way for rows and columns (double-centered PCA) or by singular value decomposition of the GE matrix (Gauch, 1992; Duarte and Vencovsky, 1999). The graphic representation of genotypes and environments is performed in an AMMI biplot, whose coordinates for each axis or principal component of GxE interaction, identified as IPCAk (k = 1, 2, ..., n), are obtained by IPCAki =
are arranged in the GE matrix and fitted in the second step via PCA. This analysis must be performed in a integrated way for rows and columns (double-centered PCA) or by singular value decomposition of the GE matrix (Gauch, 1992; Duarte and Vencovsky, 1999). The graphic representation of genotypes and environments is performed in an AMMI biplot, whose coordinates for each axis or principal component of GxE interaction, identified as IPCAk (k = 1, 2, ..., n), are obtained by IPCAki =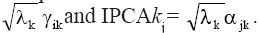
Three methods were assessed for the environmental stratification. One of them was based on the proposal of Horner and Frey (1957), and the others on AMMI analysis, associated with further developments applied to this subject (Gauch, 1990; Gauch and Zobel, 1997).
In the first method, the locations were grouped via joint ANOVA for location pairs in each year, within the maturity groups. Thus, e(e-1)/2 paired analyses were carried out for each group, and the significance (P value) of the F-test for the GxE interaction was used as a measure of similarity between each pair of locations. The log (P value) statistic, also adopted by Wilson et al. (2000), was used to solve problems in the construction of the dendrograms with very low probability values. The hierarchical agglomerative method was used for clustering, based on the UPGMA criterion. In each dendrogram, three cut-off points were taken corresponding to the significance levels (α) equal to 10, 1, and 0.1%.
In the second method, the locations were clustered using information of GxE interaction matrix resulting from the AMMI1 model analysis that selects only the first main interaction axis. The use of this model for mega-environment analysis has been proposed by Gauch (1992) and Ebdon and Gauch (2002). In this matrix, each element 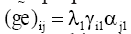 is an estimate of the specific interaction. The difference between these estimates, taking into account two locations j and j’ for the same genotype i, is a measure of the dissimilarity between these locations. Thus, considering all the genotypes, the following distance measure was adopted:
is an estimate of the specific interaction. The difference between these estimates, taking into account two locations j and j’ for the same genotype i, is a measure of the dissimilarity between these locations. Thus, considering all the genotypes, the following distance measure was adopted: 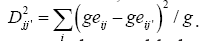 A matrix of distances among locations was used to construct the dendrogram that enabled visualization of the relative similarities among the locations, as well as to establish the environmental strata. For better visualization of the clusters, the distance
A matrix of distances among locations was used to construct the dendrogram that enabled visualization of the relative similarities among the locations, as well as to establish the environmental strata. For better visualization of the clusters, the distance 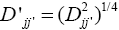 was used instead of
was used instead of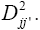 Furthermore, the cut-off in the dendrogram was defined to always obtain around of five strata, as advocated by Gauch (1992).
Furthermore, the cut-off in the dendrogram was defined to always obtain around of five strata, as advocated by Gauch (1992).
The third stratification method was based on the “winning genotype” approach (Gauch and Zobel, 1997). The analysis consists of fitting a family of AMMI models, rather than a single model, from which one is selected for the final fitting. Frequently, AMMI1 or AMMI2 are accurate, although occasionally a higher order model may be used for greater predictive accuracy. The use of the AMMI1 model for environmental stratification has been defended (Ebdon and Gauch, 2002), and therefore, it was adopted in this study. Thus, the yield AMMI1 estimates 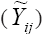 were obtained for each genotype by environment combination, which allowed the identification of the winner genotype in each environment. Consequently, each genotype with one or more wins determines an environmental stratum.
were obtained for each genotype by environment combination, which allowed the identification of the winner genotype in each environment. Consequently, each genotype with one or more wins determines an environmental stratum.
The AMMI1 yield estimates for each genotype in each environment can be equated as 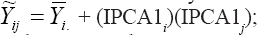 where
where 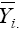 is the mean of the ith genotype in all the environments, and IPCA1i and IPCA1j are, respectively, the scores of the ith genotype and jth environment on the first interaction principal axis (IPCA1). Thus,
is the mean of the ith genotype in all the environments, and IPCA1i and IPCA1j are, respectively, the scores of the ith genotype and jth environment on the first interaction principal axis (IPCA1). Thus,  can be represented as a simple linear function of the environmental score (IPCA1j), that is, a straight line equation with intercept
can be represented as a simple linear function of the environmental score (IPCA1j), that is, a straight line equation with intercept 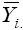 and slope equal to the genotype score (IPCA1i). In these linear regressions, the intersection between two straight lines, when associated with two winning genotypes (i and i’), defines the transition between two strata. This transition point can be estimated by
and slope equal to the genotype score (IPCA1i). In these linear regressions, the intersection between two straight lines, when associated with two winning genotypes (i and i’), defines the transition between two strata. This transition point can be estimated by 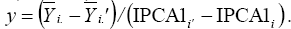 In this case, the environments are represented in a scatter plot, and each y point enables to separate two adjacent strata (Gauch and Zobel, 1997). Thus, the environmental strata were graphically established using the software developed for this kind of analysis - AMMIWINS (Gauch, 1996).
In this case, the environments are represented in a scatter plot, and each y point enables to separate two adjacent strata (Gauch and Zobel, 1997). Thus, the environmental strata were graphically established using the software developed for this kind of analysis - AMMIWINS (Gauch, 1996).
Results
The magnitude of the variation associated with the main effects (genotypes-G, and environment-E) and GxE interaction was always significant (P value < 0.05) by the F-test. The local source explained about 80% of the variation in treatments (G + E +GE), followed by GxE interaction, which accounted for 15 to 30% of this variation. Genotypes accounted for around 3 to 13% of this variation. These proportions were similar to those reported in other studies (Mortazavian et al., 2014; Ndhlela et al., 2014; Branquinho et al., 2014; Kachapur et al., 2016). Although the GxE interaction was not very high, even in these cases, selection gains can be expected through efficient environment stratification.
Environmental stratification by Horner and Frey method
Figure 1 presents the cluster dendrograms obtained by Horner and Frey (1957) method for each growing season and maturity group. Regardless of genotype or maturity groups, the number of strata increased with the adoption of higher significance (α) levels. If α = 10% was chosen, the breeder should be aware of the greater risk of type I error in his decision, that is, to suggest non-existent strata. Similarly, lower levels of probability (e.g., α = 0.1%) would result in a smaller number of strata and a greater rate of type II error. Thus, it increases the risk of grouping locations that should remain separated, and eliminate true environment strata.
Figure 1: Dendrograms of the environmental stratification for soybean inbred lines assessed in the Central Brazil region in different growing seasons (2000 to 2002) for early, medium, and late maturity groups, obtained by Horner and Frey (1957) method (horizontal lines 1, 2, and 3 are cut-offs corresponding to the 10, 1, and 0.1% of probabilities, respectively, associated with significance levels for F-statistic of the mean square of GxE interaction). The dendrograms were truncated at -log (P valor) = 4, which corresponds to a P value ≤ 0.0001.
Taking into account the main goal of this study, a consistent environmental stratification over time, in Figure 1, it is observed that these clusters have low repeatability, undoing from one growing season to another. This inconsistency across the growing seasons precludes the practical use of the stratifications obtained by this method for planning the trial network and regionalizing the cultivar recommendation in future years. Consequently, the method was deemed unsuitable for this study.
Environmental stratification by AMMI D'jj, distance
The lack of repeatability among the groupings identified at each of the growing seasons was also observed when the D'jj, distance measure was used (Figure 2). A few locations remained in the same stratum in the three growing years for each maturity group. In the early genotype maturity group, the required consistency was observed only in two clusters of locations: Anápolis/Sacramento and Buritis/Rio Verde/Lucas do Rio Verde. In the medium maturity group, the clusters Anápolis/Mineiros and Lucas do Rio Verde/Uberaba were maintained across the three growing years. In the late maturity group, temporal consistency was observed in the clusters Conquista/Uberaba and Anápolis/Capinópolis/Mineiros/Placas/ Rio Verde. These results, although better than ones obtained by Horney and Frey method, were also not satisfactory in providing a reliable recommendation of environmental zoning for the target region.
Figure 2: Dendrograms of the environmental stratification for soybean inbred lines in the Central Brazil region in different growing seasons (2000 to 2002) for early, medium, and late maturity groups, obtained by the distance measure (D’) derived from AMMI1estimates of the GxE interaction (continuous horizontal line in each graphic are the cut-offs adopted for stratification with around five strata).
Environmental stratification by ‘winning genotype’ approach
By the approach of winning genotypes and AMMI1 estimates of grain yield, from a total of eighteen locations, eight, six, and seven strata were obtained for early (Figure 3), medium (Figure 4), and late (Figure 5) maturity groups, respectively. This approach enabled the formation of three stable clustersover time for early and medium maturity groups, and four of these clusters for late maturity group. These clusters included 13 of the 18 locations in the early genotype group and 15 in each one of the medium and late groups. The results showed that the strata formed had predictive value because they were repeatable across 3years of study. It should be emphasized, however, that this stratification was carried out based only on grain yield. Other traits, such as plant diseases, for example, can modify this scenario regarding the release of a cultivar.
Figure 3: Environmental stratification for assessment of soybean lines in early maturity group, based on the winning genotype approach, associated with the AMMI1 model analysis (horizontal lines within graphics are the transitions between two adjacent strata, and circles in the same color indicate a group of locations in the same stratum).
Figure 4: Environmental stratification for assessment of soybean lines in medium maturity group, based on the winning genotype approach, associated with the AMMI1 model analysis (horizontal lines within graphics are the transitions between two adjacent strata, and circles in the same color indicate a group of locations in the same stratum).
Figure 5: Environmental stratification for assessment of soybean lines in late maturity group, based on the winning genotype approach, associated with the AMMI1 model analysis (horizontal lines within graphics are the transitions between two adjacent strata, and circles in the same color indicate a group of locations in the same stratum).
The eventual need to adopt more parameterized models also was evaluated (Tables 2 and 3). The additional variation associated with other axes IPCA, above of AMMI1 (IPCA2 to IPCA4), decreased the repeatability of the clusters gradually. Pairs of locations that were grouped in all three growing seasons when the AMMI1 model was used, began to be grouped for a shorter period when models more parameterized were used (e.g., site 14 and site 2, with model AMMI2), or even stopped grouping (e.g., site 14 and site 2, with AMMI3 and AMMI4 models). Therefore, the AMMI1 model offered greater repeatability of clusters, reinforcing the argument of some authors (Gauch, 1990, 1992; Ebdon and Gauch, 2002).
| Site | AMMI1 | Site | AMMI2 | |||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |||
| 1 | 1 | |||||||||||||||||||||||||||||||||||
| 2 | 2 | |||||||||||||||||||||||||||||||||||
| 3 | 2 | 3 | ||||||||||||||||||||||||||||||||||
| 4 | 2 | 4 | ||||||||||||||||||||||||||||||||||
| 5 | 3 | 2 | 2 | 5 | 2 | |||||||||||||||||||||||||||||||
| 6 | 3 | 2 | 2 | 3 | 6 | 3 | ||||||||||||||||||||||||||||||
| 7 | 7 | 2 | 2 | |||||||||||||||||||||||||||||||||
| 8 | 2 | 8 | 2 | 2 | ||||||||||||||||||||||||||||||||
| 9 | 2 | 2 | 2 | 2 | 9 | 2 | ||||||||||||||||||||||||||||||
| 10 | 2 | 2 | 2 | 2 | 3 | 10 | 2 | 3 | ||||||||||||||||||||||||||||
| 11 | 2 | 2 | 2 | 2 | 3 | 3 | 11 | 2 | 3 | 3 | ||||||||||||||||||||||||||
| 12 | 3 | 2 | 3 | 3 | 2 | 2 | 2 | 12 | 2 | |||||||||||||||||||||||||||
| 13 | 3 | 2 | 3 | 3 | 2 | 2 | 2 | 3 | 13 | 3 | 3 | |||||||||||||||||||||||||
| 14 | 3 | 2 | 3 | 3 | 2 | 2 | 2 | 3 | 3 | 14 | 2 | 2 | 2 | 2 | 2 | |||||||||||||||||||||
| 15 | 15 | 3 | 2 | |||||||||||||||||||||||||||||||||
| 16 | 2 | 2 | 2 | 2 | 2 | 16 | 2 | 2 | 2 | 2 | 2 | 2 | ||||||||||||||||||||||||
| 17 | 2 | 3 | 2 | 17 | 2 | |||||||||||||||||||||||||||||||
| 18 | 2 | 18 | 2 | 2 | ||||||||||||||||||||||||||||||||
| ` | ||||||||||||||||||||||||||||||||||||
1The consistency of the stratification is given by the number of times (2 or 3) in which each pair of locations is grouped together across the growing seasons. 21 (Anápolis); 2 (Chapadão do Céu); 3 (Cristalina); 4 (Luziânia); 5 (Mineiros); 6 (Rio Verde); 7 (Senador Canedo); 8 (Correntina); 9 (Placas); 10 (Pamplona); 11 (Planaltina); 12 (Buritis); 13 (Capinópolis); 14 (Iraí de Minas); 15 (Sacramento); 16 (Uberaba); 17 (Uberlândia); 18 (Lucas do Rio Verde).
Table 2: Consistency1 in which pairs of locations (sites)2 are clustered in the same stratum across of growing seasons, according to winning genotype approach, using AMMI1 and AMMI2 models for yield multi-environment trials of soybean lines and cultivars from medium maturity group assessed in the tropics of Central Brazil.
| Site | AMMI3 | Site | AMMI4 | ||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||
| 1 | 1 | ||||||||||||||||||||||||||||||||||
| 2 | 2 | ||||||||||||||||||||||||||||||||||
| 3 | 3 | ||||||||||||||||||||||||||||||||||
| 4 | 4 | ||||||||||||||||||||||||||||||||||
| 5 | 5 | ||||||||||||||||||||||||||||||||||
| 6 | 2 | 6 | 2 | ||||||||||||||||||||||||||||||||
| 7 | 7 | 2 | |||||||||||||||||||||||||||||||||
| 8 | 8 | ||||||||||||||||||||||||||||||||||
| 9 | 2 | 9 | |||||||||||||||||||||||||||||||||
| 10 | 10 | ||||||||||||||||||||||||||||||||||
| 11 | 2 | 2 | 11 | 2 | |||||||||||||||||||||||||||||||
| 12 | 12 | ||||||||||||||||||||||||||||||||||
| 13 | 2 | 2 | 13 | 3 | 2 | 2 | |||||||||||||||||||||||||||||
| 14 | 2 | 14 | |||||||||||||||||||||||||||||||||
| 15 | 2 | 2 | 15 | 2 | |||||||||||||||||||||||||||||||
| 16 | 2 | 3 | 16 | ||||||||||||||||||||||||||||||||
| 17 | 2 | 2 | 17 | 2 | |||||||||||||||||||||||||||||||
| 18 | 2 | 2 | 2 | 2 | 18 | 2 | 2 | ||||||||||||||||||||||||||||
1The consistency of the stratification is given by the number of times (2 or 3) in which each pair of locations is grouped together across the growing seasons. 21 (Anápolis); 2 (Chapadão do Céu); 3 (Cristalina); 4 (Luziânia); 5 (Mineiros); 6 (Rio Verde); 7 (Senador Canedo); 8 (Correntina); 9 (Placas); 10 (Pamplona); 11 (Planaltina); 12 (Buritis); 13 (Capinópolis); 14 (Iraí de Minas); 15 (Sacramento); 16 (Uberaba); 17 (Uberlândia); 18 (Lucas do Rio Verde).
Table 3: Consistency1 in which pairs of locations (sites)2 are clustered in the same stratum across of growing seasons, according to winning genotype approach, using AMMI3 and AMMI4 models for yield multi-environment trials of soybean lines and cultivars from medium maturity group assessed in the tropics of Central Brazil.
The criterion of eliminating smaller winner genotypes (winners in only one location) might be adopted without significant yield loss (in this case, the winner genotype could be replaced by another winner in the neighboring stratum, without large losses of grain yield), and with practical gains related to the definition of small number of manageable strata. The strata definition can be visualized in graphs, such as those shown in Figures 3, 4, and 5, where some locations are situated closer to the transition (horizontal lines) between two strata. Thus, it is possible to assess the yield losses in each location, for example, by joining two adjacent strata and recommending only one of the winner genotypes.
There were also cases in which clustering was held in two growing seasons, but not in the third years because these locations were slightly away from the transition line between two strata. For example, for the medium-maturity group in the year 2002, the locations Uberaba and Lucas do Rio Verde are in the same stratum as Buritis, Cristalina, Correntina, Planaltina, Placas, and Rio Verde (Figure 4). However, in 2000 and 2001, although Uberaba and Lucas do Rio Verde remained in the same stratum, they are separated from the other locations, but still very close to the transition line with the larger stratum. The yield loss estimate in Uberaba and Lucas do Rio Verde caused by the replacement of the original winner by the recommendation of another genotype with the slightly lower performance was below 1.5%. In other cases in which this artifice was necessary, the yield reductions estimated were less than 4%, and often not more than 1.5% (Figure 6). Therefore, a stratification strategy that takes in to account such elements is fully justified when it is desired to have a feasible zoning for breeding programs, on the real possibility of dividing the target region of inferences.
Figure 6: Yield losses of the locations with changes of strata adopted by replacement of the original winner genotype by a winner genotype of a neighboring stratum (codes of the location in the abscissa: M, E, and L are medium, early, and late maturity groups, respectively; 2000, 2001, and 2002 are the growing years).
Table 4 presents the environmental strata recommended according to the winning genotype approach, taking into account the different maturity groups of soybean lines. Two pairs of locations, Lucas do Rio Verde/Rio Verde and Cristalina/Placas, remained clustered in the three maturity groups; this means that cultivar recommendation may be the same for these pairs of locations regardless of maturity group of genotypes. Furthermore, Iraí constituted a particular stratum for the three maturity groups, corroborating the results of the other clustering methods.
| Early maturity | Medium maturity | Late maturity |
| Buritis | Buritis | Anápolis |
| Capinópolis | Correntina | Capinópolis |
| Correntina | Cristalina | Chapadão do Céu |
| Lucas do Rio Verde | Lucas do Rio Verde | Conquista |
| Rio Verde | Placas | Lucas do Rio Verde |
| (Apiakas) | Planaltina | Mineiros |
| Rio Verde | Rio Verde | |
| Uberaba | Senador Canedo | |
| (Msoy-8411) | (BR97-11548) | |
| Cristalina | Anápolis | Buritis |
| Luziânia | Capinópolis | Luziânia |
| Mineiros | Sacramento | (BR97-11548) |
| Placas | Senador Canedo | |
| Sacramento | (BRA97-6705) | |
| (MG BR97-2545) | ||
| Anápolis | Luziânia | Correntina |
| Pamplona | Mineiros | Cristalina |
| Uberlândia | Pamplona | Placas |
| (MG BR97-2545) | (BRA97-6705) | (BR97-11548) |
| - | - | Pamplona |
| Planaltina | ||
| (BR95-28822) | ||
| Irai | Irai | Irai |
| (MGBR97-2545) | (GO BR97-15587) | (GO BR97-08728) |
| Chapadão do Céu | Chapadão do Céu | - |
| (Apiakas) | (Msoy-8411) | |
| Uberaba | - | Uberaba |
| (GO BR96-014101) | (GOBR97-08728) | |
| - | Uberlândia | - |
| (GO BR97-15587) | ||
| - | - | Sacramento |
| (BR97-11548) | ||
| Planaltina | - | - |
| (Apiakas) | ||
| Senador Canedo | - | - |
| (MG BR97-2545) | ||
| strata number = 8 | Strata number = 6 | Strata number = 7 |
1The cultivar recommendation was based on the last growing season (the year 2002).
Table 4: Agronomic zones or mega-environments for assessment and recommendation of soybean genotypes in the Central Brazilian region, established by winning genotype approach for environmental stratification, taking account three maturity groups (the recommended cultivar for each stratum and maturity group is indicated in the center of table cells, within parentheses)1.
Furthermore, a slightly larger number of locations remained grouped when two maturity groups were considered. For early and medium maturity, four locations could be maintained in the same stratum: Buritis, Correntina, Lucas do Rio Verde, and Rio Verde. Thus, the cultivar recommendations for this mega-environment can be uniform in these two maturity groups. For the medium and late maturity groups, three locations always appeared in the same strata: Anápolis, Capinópolis, and Senador Canedo. Thus, it can also be characterized as a further environmental stratum suitable for uniform cultivar recommendations in these maturity groups. At last, as expected from the more diverging maturity groups, early and late, any stratum was consistent for both (Table 4).
Discussion
As already mentioned, the source of variation related to locations accounts for most of the G+E+GE variation, but this did not constitute a variation source responsible for changing the ranking of genotypes due to its additive effect. For the same reason, the variation attributable to genotypic effects, although also significant, does not influence the formation of strata. However, the significant GxE interaction indicates that the performance of the soybean lines was not consistent in the different locations. Therefore, the environmental stratification was justified and it would also justify studies of phenotypic adaptability and stability.
Practically, for a useful stratification of a wide cropping region, it is important that the number of recommended strata be reasonably stable and small. This concept of stability includes its repeatability over time, and the possibility of the stratification being valid even with changes of genotypes across the years (this requirement justified the assumption of random effects for genotype effects). In this sense, the results obtained with the winning genotype approach are encouraging enough. In all the maturity groups, clusters of locations with temporal consistency were identified. For the early and medium groups, this approach provided three of the more stable clusters and for the late-maturity genotypes, four stable environmental strata were produced (Table 4). These results agree with those obtained by other authors, in environmental stratification studies for sorghum grain yield (Rakshit et al., 2012), barley (Mohammadi et al., 2009; Mortazavian et al., 2014), and maize (Oyekunle et al., 2017). The AMMI1 model offers greater repeatability of the clusters, concerning more parameterized AMMI models, which incorporate more axes of the GxE interaction (Gauch, 1990, 1992; Ebdon and Gauch, 2002). The predictive accuracy achieved by increasing the number of principal components associated with the AMMI model decreases, which is equivalent to a reduction in the number of replications (Ebdon and Gauch, 2002; Gauch, 2006); this explains the greater repeatability of the clusters identified by the winning genotypes approach when the AMMI model is not super-parametrized (Tables 2 and 3). Additionally, this can be understood as the combined result of two characteristics: i) the capacity of AMMI model to capture, in the first interaction axes, a greater proportion of the variability pattern existing in the dataset; and ii) the characteristic of this method to concentrate the decision making on a smaller set of genotypes of greater interest, only the winner genotypes. Thus, the responses of those genotypes that do not help clarify the scenario are relegated to a secondary position (Ebdon and Gauch, 2002).
The stratification based on this approach enabled an integrated understanding of the genotypic and environmental performance. Therefore, the objective of identifying environmental strata was reached at the same time as the identification of genotypes with specific adaptation to the constituted strata. Thus, the recommendation of cultivars is directly associated with the regionalization (Table 4).
Results that lead to a consistent stratification over time are of interest to breeders and seed and grain producers. Breeding programs have their efficiency increased with the most appropriate choice of experimental sites, as well as the identification of specific adaptation genotypes in the target environment population. In turn, seed producers can develop more regionalized markets, building their business reserve in a specific microregion (stratum). At the end of the chain, the grain producers are also benefited by better results from the research programs, and by the seed offer from suppliers in their region.
Conflicts of interest
The authors declare no conflict of interest.
Acknowledgments
The authors thank Embrapa, particularly the researchers of soybean breeding program of Embrapa Cerrados, and Convênio Cerrados (Embrapa/AgênciaRural/Centro Tecnológico para Pesquisas Agropecuárias - CTPA) for providing the data used in this study.
About the Authors
Corresponding Author
R.G. Branquinho
Escola de Agronomia, Centro de Excelência em Melhoramento da Cana-de-Açúcar, Universidade Federal de Goiás, Goiânia, GO, Brasil
- Email:
- rodrigogobr@bol.com.br
References
- Branquinho RG, Duarte JB, Souza PIM, Silva Neto SP, et al. (2014). Estratificação ambiental e otimização de rede de ensaios de genótipos de soja no Cerrado. Pesqui. Agropecu. Bras. 49: 783-795. https://doi.org/10.1590/S0100-204X2014001000005
- Duarte JB and Vencovsky R (1999). Interação genótipos x ambientes: uma introdução à análise AMMI. Sociedade Brasileira de Genética, Ribeirão Preto. Available at https://agro.ufg.br/up/396/o/Monografia_9_ammi_sbg.pdf]. Accessed March 26, 2017.
- Ebdon JS and Gauch HG (2002). Additive Main Effect and Multiplicative Interaction Analysis of National Turfgrass Performance Trials: II Cultivar Recommendations. Crop Sci. 42: 497-506. https://doi.org/10.2135/cropsci2002.0497
- Gauch Jr HG (1990). Full and reduced models for yield trials. Theor. Appl. Genet. 80: 153-160. https://doi.org/10.1007/BF00224379
- Gauch HG (1992). Statistical analysis of regional yield trials: AMMI analysis of factorial designs. Elsevier, New York.
- Gauch HG (1996). Documentation for AMMIWINS. Available at [http://microcomputerpower.com/ammiwins.html]. Accessed November 30, 2016.
- Gauch HG (2006). Statistical analysis of yield trials by AMMI and GGE. Crop Sci. 46: 1488-1500. https://doi.org/10.2135/cropsci2005.07-0193
- Gauch HG and Zobel RW (1997). Identifying mega-environments and targeting genotypes. Crop Sci. 37: 311-326. https://doi.org/10.2135/cropsci1997.0011183X003700020002x
- Hartley HO (1950). The maximum F-ratio as a short-cut test for heterogeneity of variance. Biometrika 37: 308-312.
- Horner TW and Frey KJ (1957). Methods for determining natural areas for oat varietal recommendations. Agron. J. 49: 313-315. https://doi.org/10.2134/agronj1957.00021962004900060009x
- Kachapur RM, Wali MC, Basavaraj GT and Patil BS (2016). Studies on genotype x environment interaction and stability for yield in soybean (Glycine max (L.) Merrill). Electron. J. Plant Breed. 7: 803-808.
- Mohammadi R, Amri A and Ansari Y (2009). Biplot analysis of rainfed barley multienvironment trials in Iran. Agron. J.101: 789-796. https://doi.org/10.2134/agronj2008.0203x
- Mortazavian SMM, Nikkhah HR, Hassani FA, Sharif-al-Hosseini M, et al. (2014). GGE biplot and AMMI analysis of yield performance of barley genotypes across different environments in Iran. J. Agric. Sci. Technol. 16: 609-622.
- Ndhlela T, Herselman L, Magorokosho C, Setimela P, et al. (2014). Genotype × environment interaction of maize grain yield using AMMI biplots. Crop Sci. 54: 1992-1999. https://doi.org/10.2135/cropsci2013.07.0448
- Oyekunle M, Menkir A, Mani H, Olaoye G, et al. (2017). Stability analysis of maize cultivars adapted to tropical environments using AMMI analysis. Cereal Res. Commun. 44: 1-10.
- Rakshit S, Ganapathy KN, Gomashe SS, Rathore A, et al. (2012). GGE biplot analysis to evaluate genotype, environment and their interactions in sorghum multi-location data. Euphytica 185: 465-479. https://doi.org/10.1007/s10681-012-0648-6
- Romagosa I and Fox P (1993). Genotype × environment interaction and adaptation. In: Plant breeding: principles and prospects (Hayward MD, Bosemark NO, Romagosa I and Cerezo M, eds.). Chapman & Hall, London.
- Wilson CA, Kreychman J and Gerstein M (2000). Assessing annotation transfer for genomics: quantifying the relations between protein sequence, structure and function through traditional and probabilistic scores. J. Mol. Biol. 297: 233-249. https://doi.org/10.1006/jmbi.2000.3550
Keywords:
Download:
Full PDF- Share This





